정보처리기사 제1과목 데이터베이스 – 제2장 자료구조의 기본 1부
요약 정리
Ⅰ. 자료 구조와 알고리즘
1. 자료 구조(Data Structure)
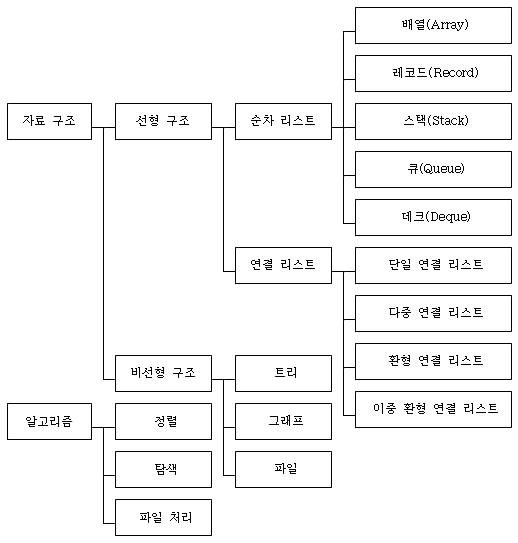
가. 자료 구조(Data Structure)의 정의
프로그램에서는 주어진 문제를 나누어서 해결하게 된다. 이때 처리될 정보는 프로그래밍 언어 구조에서 제공하고 있는 자료 구조(Data Structure)로 저장된다. 자료 구조란 알고리즘이 처리할 자료를 프로그램에서 표현하는 방법이다.
자료 구조의 예로 배열(Array), 리스트(List), 스택(Stack), 큐(Queue), 트리(Tree), 그래프(Graph) 등의 여러 가지 형태가 있다. 이들은 모두 리스트(List)와 배열(Array)이라는 기본적인 자료 구조에 의해서 표현이 가능하다. 잘 구성된 자료 구조는 문제 해결을 빠르고 쉽게 한다. 프로그래머가 어떠한 자료 구조를 선택하느냐에 따라 프로그램의 실행 속도, 기억 용량, 프로그램의 명확성 및 간결성이 달라진다.
파스칼(Pascal)을 설계하여 만든 스위스의 저명한 전산학자 니클라우스 비르트(Niklaus Wirth)의 저서 중에 ‘알고리즘(Algorithm) + 자료 구조(Data Structure) = 프로그램’ 이라는 책이 있다. 이 책의 제목은 우리가 배울 자료 구조에 대해 가장 간결하게 요약해 준다. 즉 자료 구조와 알고리즘이 정의되면 프로그램의 작성이 끝난 것이나 다름이 없다. 왜냐하면 프로그램은 자료 구조와 알고리즘(Algorithm)으로 구성되어 있기 때문이다.
나. 자료(Data)의 단위
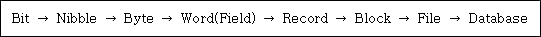
- 비트(Bit, Binary Digit): ‘0’, ‘1’의 표현으로 전산기 구조의 최소 단위이다.
- 니블(Nibble): 4개의 bit를 묶어 하나의 단위로 나타낸 것. 보통 16진수의 단위이다.
- 바이트(Byte): 8개의 bit를 묶어 하나의 단위로 나타낸 것. 문자 표현의 단위. 주소 표현의 단위이다.
- 워드(Word): 내부 처리나 표현의 위한 단위. 일반적으로 16bit, 32bit, 64bit 등으로 구성된다.
- 필드(Field): 어떤 목적을 가진 레코드(Record)나 메시지 헤더 또는 컴퓨터 명령어와 같은 데이터(Data) 단위 내의 고정된 장소이다.
- 레코드(Record): 워드(Word)나 필드(Field)가 모여서 이루는 논리적 단위이다. 내부에서 자료가 처리되는 단위.
- 블록(Block): 논리 레코드(Record)들을 묶어 I/O를 하기 위한 단위이다.
- 파일(File): 같은 종류의 레코드(Record)를 묶어 나타낸 운영체제의 액세스 단위이다. 예를 들어 고객들 개개인에 관한 사항을 하나의 파일(file)에 저장했다면, 각 레코드(record)는 ‘고객 이름’, ‘고객 번호’, ‘고객 주소’ 등과 같은 데이터 항목을 담고 있는 필드(field)로 구성될 수 있다.
- 데이터베이스(Database): 서로 관련이 있는 데이터를 통합하여 묶어 놓은 데이터 그룹이다.
다. 자료(Data)의 표현
① 수치 자료(Numeric Data)
– 정수형
- 팩 10진 형식(Pack Decimal Format)
- 언팩 10진 형식(Unpack Decimal Format)
- 고정 소수점 형식(Fixed Point Format)
– 실수형
- 부동 소수점 형식(Floating Point Format)
② 비수치 자료(Non-Numeric Data)
- BCD(Binary Coded Decimal)
- EBCDIC(Extended Binary Coded Decimal Interchange Code)
- ASCII(American Standard Code for Information Interchange)
- 가중치 코드(Weighted Code)
- 비가중치 코드(Unweighted Code)
2. 알고리즘(Algorithm)
가. 알고리즘(Algorithm)의 정의
원래는 인도에서 아랍을 거쳐 유럽에 보급된 필산을 뜻하며, 아랍의 수학자인 알콰리즈미(al-Khwārizmī)의 이름에서 유래한다. 알고리즘(Algorithm)은 어떤 문제의 해결을 위해 컴퓨터가 사용 가능한 정확한 방법을 말한다. 알고리즘은 여러 단계의 유한한 집합으로 구성되는데, 여기서 각 단계는 하나 또는 그 이상의 연산을 필요로 한다.
나. 알고리즘(Algorithm)의 필요 조건
- 명확성: 각 연산들은 명확한 의미를 가져야 한다.
- 효율성: 각 연산은 원칙적으로 일정한 시간 내에 사람이 연필로 할 수 있어야 한다.
- 입력: 외부 입력 자료가 있을 수 있다.
- 출력: 하나 이상의 결과가 나온다.
- 종결성: 유한 번의 연산 후에는 끝나야 한다.
Ⅱ. 선형 및 비선형 구조
1. 선형 구조(Linear Structure)
가. 선형 구조(Linear Structure)의 정의
파일 시스템이나 데이터베이스에서 각각의 오직 하나의 레코드(Record)만을 보유할 수 있는 구조. 즉 데이터(Data)가 연속적으로 연결되어 있는 모양으로 구성하는 방법이다.
나. 선형 구조(Linear Structure)의 종류
① 선형 리스트(Linear List)
– 선형 리스트(Linear List)의 정의
일련의 데이터 요소들을 통합하여 관리함으로써 정보의 축적과 검색 등 각종 응용 프로그램을 효율적으로 실현하기 위해 사용되는 선형 구조(Linear Structure)의 하나로, 1개의 체인(Chain), 즉 다음에 이어지는 데이터 요소를 가리키는 포인터(Pointer)를 1개만으로 표현할 수 있는 것.
– 선형 리스트(Linear List)의 종류
- 배열(Array): 컴퓨터에서 사용되는 자료 구조(Data Structure)의 한 가지로, 같은 형의 데이터(Data)들로 이루어진 집합. 배열(Array)은 처음 생성이 일정한 크기의 공간을 가진다. 따라서 데이터 개수가 몇 개가 될지 모르는 상황에서 무리한 공간 할당은 손실로 이루어질 수 있다. 또한 삽입, 삭제에 데이터의 순서를 유지하기 위해서 많은 데이터를 옮겨야 하는 부담을 가지고 있다. 하지만, 배열(Array)은 고유의 색인 번호를 가지고 있으므로 인덱스(Index) 접근이 가능하다.
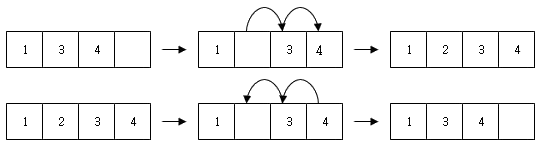
배열(Array)의 삽입과 삭제 - 레코드(Record): 서로 연관된 필드(Field)들의 집합으로 구성되어 파일의 기본 원소가 되는 자료 저장이나 표현의 기본단위.
- 스택(Stack): 자료 구조(Data Structure)의 하나로서 자료(Data)의 삽입과 삭제가 한쪽 끝에서만 일어나는 선형 리스트(Linear List). 밑이 막힌 통을 세워 놓은 것으로 생각하면 된다. 자료(Data)의 삽입, 삭제가 일어나는 곳을 스택(Stack)의 톱(Top)이라 하며 자료(Data)를 넣는 것을 푸시(Push), 스택(Stack)에서 자료를 꺼내는 것을 팝(Pop)이라 한다. 스택에서는 나중에 들어간 자료가 먼저 꺼내지므로 후입 선출(LIFO, Last Input First Output)이라고도 한다. 스택은 주로 어떤 내용을 기억시켰다가 다시 이용하고자 할 때 사용되며, 컴퓨터 알고리즘에서 자주 쓰이는 중요한 자료 구조이다. 예로써 택시를 타면 운전기사가 동전을 차례로 넣는 동전 통과 같다. 동전 통의 한쪽 끝에서 동전의 투입(삽입)과 회수(삭제)가 일어난다.
– 스택(Stack)의 특징
- 포인터(Pointer)를 한 개 두고 운용.
- LIFO 구조
- 한쪽 방향에서만 I/O하는 구조.
– 스택(Stack)의 이용
- 서브 프로그램 호출시 복귀 주소 저장.
- 인터럽트 분기시 복귀 주소 저장.
- 되부름시 복귀 주소 저장.
- 역폴리쉬(Reverse Polish Notation) 운용시.
- 주소 주소 방식으로 수식 연산시.
용어 설명
– 역폴리쉬(Reverse Polish Notation)
수식을 컴퓨터가 번역할 때 피연산자를, 연산자 앞에 놓는 기법. 예를 들면 a * (b + c)를 역폴리쉬로 표현하면 abc*+가 된다.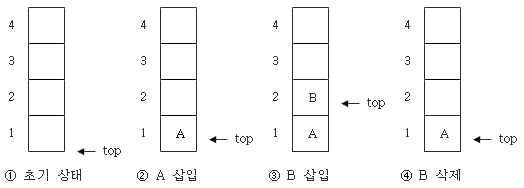
스택(Stack)의 삽입과 삭제
스택(Stack)을 수행하는 프로그램#include
#define Max 100 int stack[Max]; int top = 0; int push(int n) { if (top < Max) { stack[top] = n; top++; return(0); } else { return(-1); } } int pop(int *n) { if (top > 0) { top--; *n = stack[top]; return(0); } else { return(-1); } } void main(void) { int c; int n; while (printf("*"), (c = getchar()) != EOF) { rewind(stdin); if (c == 'i' || c == 'I') { printf("push data -> "); scanf("%d", &n); rewind(stdin); if (push(n) == -1) { printf("Stack is full\n"); } } // end of if if (c == 'o' || c == 'O') { if (pop(&n) == -1) printf("Stack is empty"); else printf("pop data -> %d\n", n); } // end of if } // end of while } Result
*input push data -> 78 push data -> 25 push data -> 90 push data -> 80 *output pop data -> 80 pop data -> 90 pop data -> 25 pop data -> 78
- 큐(Queue): 컴퓨터의 각 분야에서 가장 많이 사용되는 자료 구조(Data Structure)의 하나로서 가령 운영체제에서 작업(Job)을 처리하는 작업 스케줄링(Job Scheduling) 등과 같은 예에서처럼 사용된다. 큐(Queue)란 용어의 사전적 해석으로 ‘차례를 기다리는 줄지어 서있는 사람이나 차량의 행렬’으로 볼 수 있다. 예로써 극장 매표구 앞에 표를 사기 위해 기다리는 대기열(Queue)를 말한다. 먼저 온 사람이 표를 사서 빠져나가고(삭제), 뒤쪽 끝에는 새로운 사람들이 대기열(Queue)로 들어온다(삽입).
– 큐(Queue)의 특징
- 삽입(Rear, Tail)과 삭제(Front, Head) 포인터(Pointer) 두 개를 두고 운용.
- 한쪽 방향에서는 입력만 하고, 다른 한쪽 방향에서는 출력만 하는 구조.
- 선입 선출(FIFO) 구조.
– 큐(Queue)의 이용
- 키보드 버퍼 이용시.
- 스풀(Spool) 운용시.
- 스케줄링 작업시.
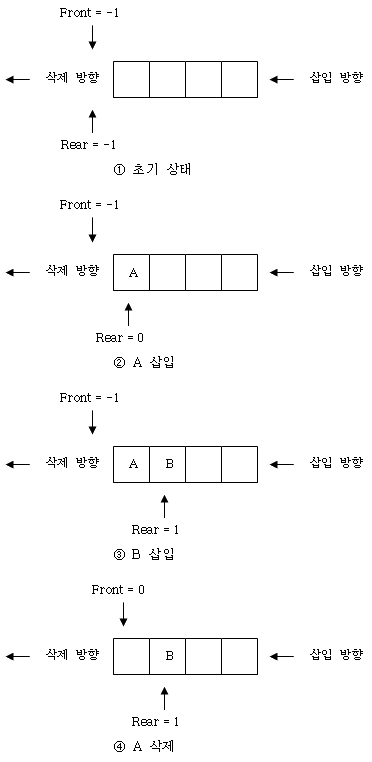
큐(Queue)의 삽입과 삭제 - 데크(Deque, Double Ended Queue): 삽입과 삭제가 양쪽 끝에서 허용되는 선형 리스트(Linear List)의 한 형태. 입력이 한쪽 끝으로만 가능하도록 제한한 데크(Deque)는 스크롤(Scroll)이라고 하고, 출력이 한쪽 끝으로만 가능하도록 제한한 데크(Deque)는 셀프(Shelf)라고 한다.
– 데크(Deque)의 특징
- 포인터(Pointer) 두 개를 두고 운용.
- 가장 일반적인 구조.
- 양쪽 끝에서 I/O가 일어나는 구조.
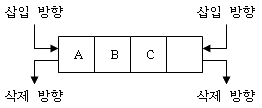
데크(Deque)
② 연결 리스트(Linked List)
– 연결 리스트(Linked List)의 정의
일련의 데이터 요소들을 통합하여 관리함으로써 정보의 축적과 검색 등 각종 응용 프로그램을 효율적으로 실현하기 위해 사용되는 선형 구조(Linear Structure)의 하나로, 각 데이터 요소가 포인터(Pointer)에 의해 다른 데이터 요소에 연결되는 리스트(List). 데이터 요소가 기억 장치 중 여기저기 분산되어 있지만 각 데이터 요소에는 리스트(List) 중 다른 데이터 요소의 기억 장소를 가리키는 포인터(Pointer)가 수용되어 있어서 그 포인터(Pointer)의 순서에 따라서 데이터 요소의 물리적 위치는 변경하지 않고 데이터 요소를 삽입, 삭제, 분할, 결합 및 검색 할 수 있고 순서를 변경할 수 있게 하는 리스트(List)이다.
– 연결 리스트(Linked List) 종류
- 단일 연결 리스트(Singly Linked List): 연결 리스트(Linked List)의 하나로 리스트의 각 노드(Node)에 리스트 중 직후의 노드를 가리키는 1개의 포인터(Pointer)가 있는 것. 기억 장소는 절약 되지만 데이터 요소를 삽입, 삭제, 탐색하는 등의 조작 효율은 다중 연결 리스트(Doubly Linked List)보다 못하다.
- 다중 연결 리스트(Doubly Linked List): 연결 리스트(Linked List)의 하나로 리스트의 각 노드(Node)에 리스트 중 직후의 노드와 직전의 노드를 가리키는 2개의 포인터(Pointer)가 있는 것. 데이터 요소를 전후 양방향으로 삽입, 삭제, 탐색하는 등의 조작이 가능하므로, 단일 연결 리스트(Singly Linked List)에 비해 기억 장소는 더 많이 필요하지만 조작 효율이 높다.
- 이중 환형 연결 리스트(Doubly Circular Linked List)
2. 비선형 구조(Nonlinear Structure)
가. 비선형 구조(Nonlinear Structure)의 정의
트리(Tree)나 그래프(Graph)와 같은 구조. 포인터(Pointer) 등을 사용하여 자료(Data)를 연결하면 그 결과를 자료(Data)가 일직선상에 표시하거나 하나의 원상에 표시하는 구조를 말한다.
나. 비선형 구조(Nonlinear Structure)의 종류
① 트리(Tree)
– 트리(Tree)의 정의
데이터를 저장하는 노드(Node)들이 계층적으로 연결되어 있는 자료 구조(Data Structure)의 하나. 가장 위쪽에 있는 노드를 뿌리(Root) 또는 뿌리 노드(Root Node)라고 한다. 뿌리(Root)는 에지(Edge)로 연결된 자식 노드(Child Node)를 가질 수 있는데, 이때에 뿌리(Root)는 자식 노드의 부모 노드(Parent Node)가 된다. 자식 노드는 또 자신의 자식 노드를 가질 수 있다. 부모가 같은 노드를 형제 노드(Sibling Node, Brother Node)라고 한다. 트리(Tree) 안의 각 노드(부모 노드를 갖고 있지 않은 뿌리 노드는 제외)에는 꼭 하나의 부모 노드가 있다. 그래서 트리(Tree) 안의 모든 노드는 뿌리 노드의 자손이 된다. 이와 같은 노드 간의 관계 때문에 뿌리 노드에서 트리(Tree) 안의 다른 어떤 노드로 가는 경로는 단 하나밖에 없다. 트리(Tree)는 트리 구조와 같은 의미를 갖는다. 트리 구조는 디스크상의 파일 시스템 관리, 데이터베이스 관리 등 여러 분야에서 널리 사용되는 자료 구조이다.
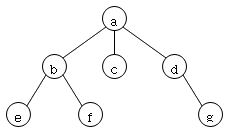
– 트리(Tree)의 용어
- 뿌리 노드(Root Node): 트리의 뿌리가 되는 노드.(예: ⓐ)
- 리프(Terminal Node, Leaf): 노드의 차수(Degree)가 0인 노드, 또는 자식이 없는 노드.(예: ⓒⓔⓕⓖ)
비단말 노드(Non-terminal Node): 노드의 차수(Degree)가 0이 아닌 노드, 또는 자식을 가지고 있는 노드.(예: ⓐⓑⓓ)
차수(Degree): 각 노드의 가지 수 – 간선 -, 또는 각 노드가 가지고 있는 자식 노드의 수.(예: ⓐ의 차수는 3, ⓑ의 차수는 2, ⓒ의 차수는 0) - 트리의 차수(Degree of Tree): 트리 전체에서 노드의 차수가 가장 큰 것을 트리의 차수(Degree)라고 한다.(예: 트리의 차수는 3)
- 레벨(Level): 뿌리 노드를 1레벨로 하여 차례로 2, 3레벨로 증가시켜서 표현한다.
- 높이(Height): 트리의 총 높이를 의미한다.(예: 트리의 높이는 3)
- 조상(Ancestors): 각 노드의 상위 레벨에 해당하는 모든 노드를 의미한다.(예: ⓖ의 조상은 ⓐ와 ⓓ이다)
- 자손(Descendants): 각 노드의 하위 레벨에 해당하는 모든 노드를 의미한다.
- 숲(Forest): 트리가 모여서 이루어진 집합을 의미한다.
- 서브 트리(Sub Tree): 임의의 노드를 제거했을 때 생길 수 있는 트리의 집합을 의미한다.
- 부모 노드(Parent Node): 각 노드의 바로 상위 레벨에 있는 노드를 의미한다.
- 자식 노드(Child Node): 각 노드의 바로 하위 레벨에 있는 노드를 의미한다.
- 형제 노드(Sibling Node, Brother Node): 같은 부모 노드에 연결되어 있는 노드를 의미한다.
– 이진 트리(Binary Tree)의 정의
모든 노드의 차수(Degree)가 2 이하인 트리(Tree). 즉, 공집합(Empty Node)이거나 1개의 뿌리 노드(Root Node)에서 왼쪽 서브 트리와 오른쪽 서브 트리로 구성된 유한 집합 구조를 말한다.
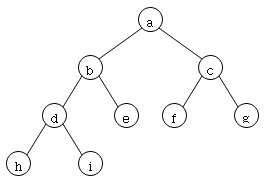
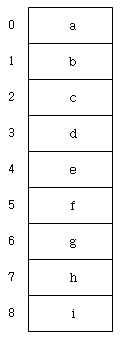
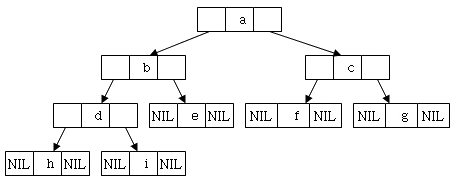
– 이진 트리(Binary Tree)의 특징
일반 트리에서는 뿌리 노드(Root Node)가 하나 있어야 트리로 간주하지만, 이진 트리(Binary Tree)에서는 공집합(Empty Node)도 트리.
- 트리의 차수(Degree) – 노드의 가지수 – 가 2 이하인 트리.
- 이진 트리(Binary Tree)는 자식 노드(Child Node)의 순서를 구분하는 순서 트리(Ordered Tree).
- NIL(Null Link)의 개수는 n+1개이고 전체 링크의 개수가 2n개이므로 NIL의 점유율은 약 1/2.(그림 10, 에서 노드의 수는 9개, NIL의 개수는 10개, 전체 링크의 개수는 18개)
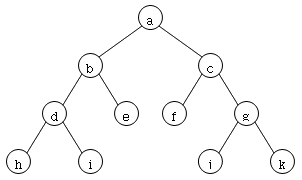
– 트리 운행법(Tree Traversal)
- 중위 운행법(Inorder, LVR): 좌 근 우측 순서로 운행하는 방법으로 ⓗⓓⓘ ⓑⓔ ⓐ ⓕⓒ ⓙⓖ ⓚ로 운행한다.
- 전위 운행법(Preorder, VLR): 근 좌 우측 순서로 운행하는 방법으로 ⓐⓑⓓⓗ ⓘⓔ ⓒⓕ ⓖⓙⓚ로 운행한다. (예: 중위 표현식 A/B+C+D+E의 전위 표현식은 +**/ABCDE이다.)
- 후위 운행법(Postorder, LRV): 좌 우 근 순서로 운행하는 방법으로 (ⓗⓘⓓ)ⓔⓑ ⓕⓙ ⓚⓖⓒⓐ로 운행한다. (예: 중위 표현식 A/B+C+D+E의 후위 표현식은 AB/C*D*E+이다.)
용어 설명
– 폴리쉬 표기법(Polish Notation)
컴퓨터에 수식을 표기할 때, 피연산자를 연산자 뒤에 놓는 표기 방법. 예를 들면 아래와 같다.
infix(대상 연산자 대상): 2 + 3 Inorder 운행
prefix(연산자 대상 대상): + 2 3 Preorder 운행
postfix(대상 대상 연산자): 2 3 + Postorder 운행– 스레드 이진 트리(Thread Binary Tree)의 정의
n개의 노드를 가진 이진 트리(Binary Tree)를 연결 리스트(Linked List)를 사용하여 표현할 때 연결 부분 중 사용하지 않는 n + 1의 NIL을 저장하기 위해 기억공간이 낭비된다. 그래서 NIL부분을 포인터(Pointer)로 바꿔 다른 노드를 가리키게 한다. 이 포인터(Pointer)를 스레드(Thread)라고 한다.– 스레드 이진 트리(Thread Binary Tree)의 특징
비순환적인 이진 트리(Binary Tree) 운행 알고리즘에서 스택을 사용하지 않고 낭비되는 NIL를 활용하여 운영하도록 고안된 이진 트리(Binary Tree).Perlis. Thornton에 의해 NIL을 이용하는 방법이 고안되었다.
실제 포인터(Pointer)와 스레드(Thread)를 구별하기가 어렵다.
② 그래프(Graph)
– 오일러 행로(Eulerian Walk)
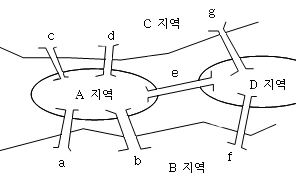
그래프(Graph) 이론을 최초 사용. 모든 간선(Edge)을 한 번씩만 경유하여 원래의 출발 정점으로 되돌아오는 길. 1736년 스위스(Suisse)의 수학자 오일러(Euler)가 쾨니히스베르크(Köigsberg) – 도이츠(Deutschland) 지역이었을 때의 이름 – 에 있는 프레겔(Pregal) 강의 7개 다리를 한 번씩만 경유하여 원래 출발점으로 되돌아오는 문제를 해결하는 데 사용한 방법이다.
예를 들어 B지역을 출발하여 모든 다리를 한번씩만 건너서 다시 B지역으로 오는 과정을 생각해보면, B를 출발하여 다리 a를 거쳐 A지역으로, e를 거쳐 D로, g를 거쳐 C로, d를 거쳐 다시 A로, b를 거쳐 B로, f를 거쳐 D지역에 도달한다. 그러나 B로는 되돌아 갈수는 없게 된다. 따라서 오일러(Euler)는 모든 다리를 단 한 번씩만 거쳐서는 결코 출발했던 지점으로 되돌아 올 수 없다는 사실을 알게 되었다. 오일러(Euler)는 각 지역을 정점(vertex)으로, 다리를 간선(edge)으로, 정점에 접한 간선의 수를 정점의 차수(Degree)라고 생각하여 문제를 해결했다. 즉, 각 정점의 차수가 짝수일 경우에만 임의의 정점에서 출발하여 각 간선을 단 한번씩만 거치고 출발한 정점으로 되돌아올 수 있다는 것을 발견했다. 이런 경로를 오일러 행로(Eulerian Walk)라고 한다. 따라서 이 다리는 4개 정점 – A, B, C, D지역 – 의 차수가 모두 홀수이므로 오일러 행로(Eulerian Walk)는 존재하지 않는다.
– 그래프(Graph)의 정의
자료 요소에 해당하는 정점(Vertex, V, Node)과 정점간의 관계를 표시하는 간선(Edge, E)으로 구성. 그래프(Graph) G = (V, E)로 표현한다.
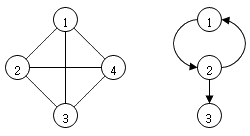
– 그래프(Graph)의 종류
무방향 그래프(Undirected Graph): 정점(vertex)간의 간선(edge)이 방향성을 갖고 있지 않는 그래프(Graph). 따라서 (V₁, V₂)와 (V₂, V₁)은 같은 간선(edge)이다.
방향 그래프(Directed Graph): 정점(vertex)간의 간선(edge)이 방향성을 갖고 있는 그래프(Graph). (V₁, V₂)로 나타내며 V₁은 간선(edge)의 시작, V₂는 간선의 끝을 나타낸다. 따라서 (V₁, V₂)와 (V₂, V₁)는 다른 간선(edge)이다.
– 그래프(Graph)의 표현 방법
인접 행렬(Adjacent Matrix): 각 정점(Vertex)들 간의 연결 상태를 행렬과 같은 형태로 나타내는 방법. 정점의 개수가 n개일 때 인접 행렬(Adjacent) M은 정사각형 행렬 형태를 띤다. i행, j열의 값이 1이면 i와 j에 해당하는 정점이 인접해 있는 것이고, 그 값이 0이면 인접하지 않는 것이다. 예를 들어 3행, 2열의 값이 1이면 3행에 해당하는 정점 C와 2열에 해당하는 정점 B가 인접해 있다는 것을 나타낸다. 간선 (Vi, Vj) – 방향 그래프일 경우에는 <Vi, Vj> – 가 E(G)에 속하면 A[i][j] = 1이 되고, 속하지 않으면 A[i][j] = 0으로 표현한다.
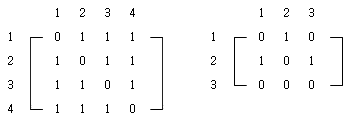
인접 리스트(Adjacent List)
인접 다중 리스트(Adjacent Multilist)
– 그래프(Graph) 운행법
깊이 우선 탐색(DFS, Depth First Search): 그래프(Graph) 탐색 방법 중의 하나로서 한 정점 v을 방문한 후에 그에 인접하고, 아직 방문하지 않은 한 정점 w를 선택하여, 다시 w를 시작점으로 깊이 우선 탐색(DFS)을 한다. 만일 이전 과정에서 모든 인접 정점들이 이미 방문했던 정점 v에 도달할 때에는, 방문하지 않은 인접 정점 w를 가졌던 제일 마지막 정점으로 되돌아가 정점 w부터 다시 깊이 우선 탐색(DFS)을 시작하는 방법.(예: 그림 13의 G₁에 대한 DFS는 1, 2, 4, 3이다)
너비 우선 탐색(BFS, Breath First Search): 시작 정점 v를 방문한 후 시작 정점 v에 인접한 모든 정점들을 우선 방문하는 방법. 더 이상 방문하지 않은 점점이 없을 때까지 방문하지 않은 모든 정점들에 대해서도 넓이 우선 탐색(BFS)을 적용한다.(예: 그림 13의 G₁에 대한 BFS는 1, 2, 3, 4이다)
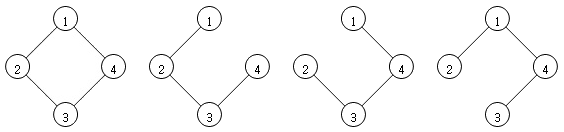
– 스패닝 트리(Spanning Tree)
연결된 비방향성 그래프(Undirected Graph) G(V, E)에서 순환 경로를 제거하면서, 연결된 부분 그래프가 되도록 이음선을 제거하면 스패닝 트리(Spanning Tree)가 된다. 따라서 스패닝 트리(Spanning Tree)는 G안에 있는 모든 정점을 다 포함하면서 트리가 되는 연결된 부분 그래프이다.
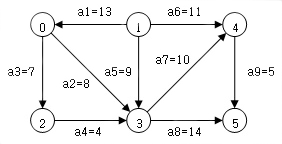
– 임계 경로(Critical Path)
여러 단계의 과정을 거치는 작업에서 그것을 완성하려면 여러 과정의 경로가 동시에 수행되어야 한다고 할 때, 그 중 가장 긴 경로, 즉, 전체 공정 중 시간이 가장 많이 걸리는 경로이다. 각 작업의 공정을 그래프 형태로 나타냈을 때 임계 경로(Critical Path)는 시작점에서 종료점에 이르는 가장 긴 경로가 된다. 전체 작업을 끝내는 데 걸리는 시간은 임계 경로(Critical Path)의 길이와 같다. 따라서 임계 경로(Critical Path)를 분석하여 그 경로상에 있는 공정들에 집중적으로 투자하면 전체 작업을 더 빨리 끝낼 수 있다.
2부에서 계속
참고 자료
正益社 – 전산학 개론
한올출판사 – C언어로 구성한 자료구조
가메출판사 – 정보처리기사 필기 7년간 기출문제 총정리
정보통신용어사전